⚓️ 왜 수학을 알아야 하는가

안녕하세요, 에디터 잭잭입니다.

 출처: ⓒ deep daiv. 

인공지능을 공부할 때 수학이 중요하다는 이야기는 익숙하게 들리지만, 막상 왜 중요한지는 쉽게 와닿지 않을 때가 많습니다. 빠르게 발전하는 인공지능 기술 속에서 중심을 잡기 위해서는 그 바탕이 되는 수학 개념들을 이해하는 것이 필요합니다.

특히 머신러닝은 데이터를 기반으로 학습하는 기술입니다. 그런데, 왜 데이터셋의 크기가 커질수록 성능이 좋아지는지 정확히 알고 계신가요? 왜 통계학에서는 항상 ‘충분히 큰’ 표본을 강조하는 걸까요?

이러한 질문에 답하기 위해, 오늘 뉴스레터에서는 머신러닝의 작동 원리를 이해하기 위해 확률과 선형대수학에서 꼭 알아야 할 개념들을 살펴보려 해요.

먼저 인공지능과 머신러닝의 관계를 짚고, 머신러닝의 프로세스를 살펴보려고 합니다. 그리고 데이터가 많아질수록 예측이 정확해지는 이유를 설명하기 위해 중심극한정리와 큰 수의 법칙을 이해합니다. 마지막으로, 고차원 데이터를 저차원으로 축소하기 위한 방법인 특잇값 분해에 대해 알아보겠습니다.

머신러닝 ⊂ 인공지능

본격적인 내용에 들어가기에 앞서, 인공지능의 개념과 오늘 주로 다룰 머신러닝을 넓은 관점에서 바라보고자 합니다.

인공지능(AI)의 목표는 ‘인간의 지능을 모방하는 것’입니다. 이러한 목표를 달성하기 위한 방법은 시대에 따라 다양하게 시도되어 왔어요. 초창기에는 사람이 정한 규칙과 논리를 기계에 제공하는 기호주의 인공지능(Symbolic AI) 방식이 주로 사용되었고, 이후 1990년대 후반부터 2000년대 초반에는 데이터를 활용한 머신러닝(Machine Learning) 방식이 주목받기 시작했습니다. 이 시기에 서포트 벡터 머신(SVM), 선형 회귀, 로지스틱 회귀 등 현재까지도 널리 활용되는 다양한 머신러닝 기법들이 소개되었습니다.

2010년 이후에는 인공신경망 기반의 딥러닝(Deep Learning) 이 빠르게 발전했으며, 특히 2012년 이미지 인식 분야에서 AlexNet의 합성곱 신경망(CNN)이 큰 성공을 거두면서 인공지능 기술은 새로운 전환점을 맞이했습니다. 이어서 2016년에는 딥마인드의 알파고가 바둑에서 인간 챔피언을 이기며 강화학습 분야에 대한 관심이 급증하기도 했어요.

여기서 주의할 점은 인공지능(AI)와 머신러닝(ML)을 동일시해서는 안 된다는 점입니다. 머신러닝은 인공지능을 구현하는 여러 방법 중 하나이며, 특히 데이터를 기반으로 인공지능을 구축하려는 접근 방식입니다. 다시 말해, 인공지능은 더 큰 개념이고, 머신러닝은 이를 실현하는 수단 중 하나인 것이죠.

인공지능과 머신러닝의 관계를 나타낸 그림

출처: ⓒ deep daiv. 

머신러닝의 목표는 ‘데이터를 가장 잘 나타내는 함수를 찾는 것’ 입니다. 이러한 과정을 데이터에 함수를 최적화시킨다고도 할 수 있어요.

머신러닝 프로세스

그러면 이번에는 직접 머신러닝 모델을 하나 만들어볼까요?

‘키’와 ‘몸무게’, ‘성별’을 바탕으로 나이를 예측하는 머신러닝 모델을 만든다고 가정하겠습니다. 그리고 아래의 데이터에는 예측하고자 하는 ‘나이’에 대한 정보가 포함되어 있으므로 지도학습(Supervised Learning)입니다.

키, 몸무게, 성별을 바탕으로 나이를 맞출 수 있는 훈련 데이터

출처: ⓒ deep daiv. 

가장 먼저 나이를 예측할 수 있는 훈련 함수 식을 만들어야 해요. 입력의 피처는 키, 몸무게, 성별이고 출력으로 나이를 예측하고자 하므로 아래와 같은 학습 함수식을 만들 수 있습니다.

이 식은 선형회귀(Linear Regression) 모델의 기본 형태로, 입력 특성들과 나이 사이의 선형적인 관계를 가정합니다. 데이터의 피처(Feature)가 3개이므로 x1~x3가 주어지고, w0은 편향(Bias)을, w1~w3은 각 피처가 나이에 미치는 영향을 나타내는 가중치(Weight)를 의미합니다.

여기서 머신러닝의 목표는 나이를 가장 잘 맞히는 함수식을 찾는 것 입니다. 이를 위해 훈련 데이터를 바탕으로 편향과 가중치를 학습하게 되는 거죠. 이때 학습의 목표는, 실제 나이인 y_true와 예측값 y_predict 사이의 오차를 최소화하는 방향으로 가중치들을 최적화하는 것입니다.

이러한 과정을 흔히 데이터에 함수를 최적화한다고 표현하며, 이 과정을 크게 세 단계로 나타낼 수 있어요.

1. 훈련 함수(Training Function) – 입력 데이터를 바탕으로 예측값을 출력하는 함수

2. 손실 함수(Loss Function) – 예측값과 실제 값 사이의 오차를 수치화하는 기준

3. 최적화(Optimization) – 손실을 최소화하도록 함수의 파라미터를 조정하는 과정

얼마나 많은 데이터를 써야, 좋은 모델을 만들 수 있을까?

머신러닝에서 우리는 보통 전체 데이터(모집단)를 사용할 수 없습니다. 대신 모집단의 일부인 표본집단을 바탕으로 모델을 훈련하죠. 그렇다면, 단지 ‘일부 데이터’만으로도 전체를 대표할 수 있다고 말할 수 있을까요? 이 질문에 대한 통계적 근거는 중심극한정리와 큰 수의 법칙에서 찾을 수 있습니다.

중심극한정리 (Central Limit Theorem)

중심극한정리란, 모집단의 분포가 어떻든 표본 크기가 충분히 크다면 그 표본평균은 정규분포를 따른다는 정리입니다. 수식으로 표현하면 아래와 같습니다.

 X_i는 모집단에서 임의로 추출한 i 번째 표본 값을 의미합니다. 예를 들어, 키에 대한 모집단에서 5명을 뽑았다고 하면, X_1은 첫 번째 사람의 키, X_2는 두 번째 사람의 키... 이런 식으로 각각의 표본 값을 나타냅니다. 여기서 n은 표본의 개수, 즉 샘플의 크기이고, X_n bar은 표본 평균으로 X_1, X_2,…, X_n의 평균값이에요.

한편 μ는 우리가 궁극적으로 알고자 하는 모집단의 진짜 평균값을 뜻하지만, 실제로는 이 값을 정확히 알 수 없습니다. 집단 전체를 조사하는 것이 현실적으로 불가능하기 때문이죠. 그러나 중심극한정리에 따르면, 표본 평균을 통해 이 μ를 근사적으로 추정할 수 있습니다.

우리가 어떤 모집단(예: 사람 키, 나이, 시험 점수 등)에서 데이터를 여러 번 뽑아낸다고 생각해 봅시다. 이때, 각 샘플에서 여러 개의 데이터들을 평균 내면 그 값이 달라질 수밖에 없죠? 100명씩 뽑아 평균 키를 구하면 어떤 샘플은 평균이 170cm이고, 또 다른 샘플은 172cm 일 수도 있어요. 중심극한정리는 이렇게 여러 번 구한 ‘샘플 평균들’이 모이면, 그 분포가 모집단의 평균과 분산을 가지는 종 모양의 정규분포를 따른다고 말하는 겁니다.

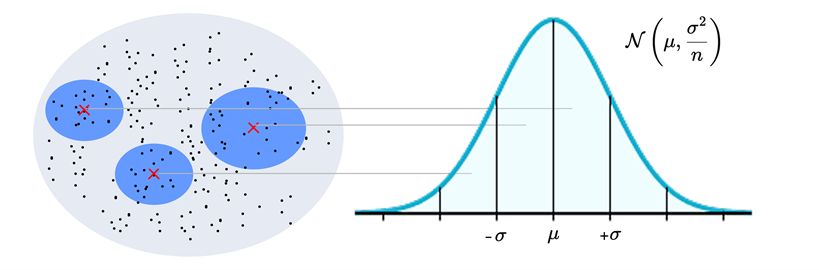
중심극한정리

출처: ⓒ deep daiv. 

따라서, 중심극한 정리는 "표본 평균들이 모집단 평균 근처에 있을 확률이 크다"는 걸 말해주는 이론으로, 여러 번 샘플링했을 때의 평균값들의 분포에 대한 이야기입니다. 그러나 실제 머신러닝에서는 보통 단 한 번의 큰 샘플(하나의 훈련 데이터셋)으로 모델을 학습시키는데, 이 하나의 표본 평균이 실제 모집단 평균에 가까운지에 대한 보장을 해주는 것은 아니에요..

큰 수의 법칙 (Law of Large Numbers)

바로 여기서 큰 수의 법칙이 필요합니다. 큰 수의 법칙은 표본의 크기(n)가 충분히 커질수록 표본 평균(X_n bar)이 모집단 평균(E[X])에 수렴한다는 것을 말합니다.

즉, 우리가 충분히 많은 데이터를 가지고 훈련 데이터를 구성했다면, 그 평균은 모집단 평균을 잘 근사할 수 있고, 이를 바탕으로 학습된 모델 역시 모집단 전체에 대해 꽤 정확한 예측을 할 수 있다는 의미예요.

따라서 표본 크기가 커질수록 모델이 관측한 데이터는 전체 모집단의 성질을 더 잘 반영하게 되며, 이를 통해 예측의 정확도 역시 높아지죠.

 큰 수의 법칙

출처: ⓒ deep daiv. 

 

정리하자면 중심극한정리는 표본 평균들이 어떤 확률 분포를 가지는지에 대한 통계적 구조를 제공하며, 큰 수의 법칙은 우리가 실제로 사용하는 하나의 큰 표본 평균이 모집단 평균과 가까워질 수 있다는 점을 보장합니다.

 

따라서 충분히 큰 표본 데이터를 통해 훈련된 함수는 전체 데이터를 대표하며, 꽤나 정확한 예측을 수행할 수 있게 되는 것입니다. 이 두 가지 원리는 머신러닝에서 왜 "데이터가 많을수록 모델이 더 정확해진다"고 말하는지를 통계적으로 뒷받침해 줍니다.

데이터가 많은 것이 무조건 좋은가

앞서 머신러닝에서 일반적으로 더 많은 데이터가 더 나은 성능을 가진다는 점을 중심극한정리와 큰 수의 법칙을 통해서 알아보았습니다. 그러나 실제로는 데이터가 너무 많아지면 계산 비용과 메모리 사용량이 급격히 증가하며, 오히려 학습 효율을 떨어뜨리기도 해요.

 

또한 데이터의 피처 수는 가중치 계산량을 증가시키는 요소입니다. 피처의 수가 늘어날수록 더 정교하게 예측할 수 있지만, 가중치 행렬의 차원이 늘어나기 때문인데요. 앞서 살펴본 키와 몸무게, 성별을 바탕으로 나이를 예측하는 선형회귀 식을 다시 가져와 보겠습니다.

 

여기에 ‘가장 좋아하는 음식’, ‘연애 횟수’, ‘재산’ 등등 피처를 계속 추가해서 총 100개의 피처가 되었다고 가정해 볼게요.

 

출력이 1차원이라고 가정하면, 데이터의 피처가 3개였을 때 가중치 행렬은 3*1 차원이었고 데이터의 피처가 100개일 때는 가중치 행렬이 100*1 차원입니다.

 

따라서 이 새로운 훈련 함수를 최적화하기 위해서는 1개의 편향과 100개의 가중치를 찾아내야 하는 거죠. 모든 훈련 데이터 포인트를 이 훈련 함수에 통과시켜 y_predict를 찾아내고, y_true와의 손실을 바탕으로 손실 함수를 최소화하는 w0~w100 값을 업데이트해야 하므로 많은 계산이 필요합니다.

 

그런데 데이터가 점점 늘어나 수백만 개의 데이터 포인트, 수천 개의 피처를 가지게 된다면 어떻게 될까요? 어떻게 하면 데이터의 정보는 유지하면서도, 더 작은 표현으로 학습할 수 있을까요?

 

이 질문에 대한 수학적 해법 중 하나가 바로 차원 축소이며, 그 대표적인 방법이 특잇값 분해(Singular Value Decomposition, SVD)입니다. SVD는 고차원 행렬을 보다 간결한 형태로 표현하면서, 데이터의 구조를 최대한 보존하는 방식으로 차원을 줄일 수 있는 강력한 수학적 도구라고 할 수 있어요.

특잇값 분해

차원 축소의 핵심은 "덜 중요한 정보를 줄이면서도 중요한 구조는 최대한 유지하는 것" 입니다. SVD는 임의의 행렬 A를 아래와 같이 세 개의 행렬 곱으로 분해합니다.

여기서,

• U는 입력 공간의 방향을 정의하는 좌측 특이벡터들의 집합,

• V는 특성 공간의 방향을 정의하는 우측 특이벡터들의 집합,

• Σ는 대각선에 특잇값(Singular Values)이 나열된 행렬로, 각 방향으로의 정보량을 나타냅니다.

 

특잇값은 행렬이 가진 정보의 '강도' 또는 '중요도'를 나타내는데, 큰 특잇값일수록 행렬의 데이터에서 더 중요한 방향(패턴)을 의미해요. 반대로 특잇값이 작으면, 그 방향은 상대적으로 덜 중요한 정보라는 뜻이죠.

 

중요한 점은 대부분의 정보가 Σ의 앞쪽, 즉 상위 몇 개의 특잇값에 몰려 있다는 것입니다. 다시 말해, Σ에 있는 특잇값들을 살펴보면 처음 몇 개는 크고 뒤로 갈수록 거의 0에 가까워지는 경우가 많습니다. 따라서 거의 0에 가까운 값들은 무시하고, 큰 값들만 남김으로써 정보의 핵심만 담은 저차원 행렬 A_r로 근사해서 표현할 수 있어요. 이렇게 하면 전체 행렬 A를 다 쓸 필요가 없어 계산은 훨씬 빨라지고, 저장 공간도 아낄 수 있으면서도 중요한 정보는 놓치지 않을 수 있는 거죠.

 

이렇게 만들어지는 근사 행렬 A_r는 원래 행렬 A와 가장 가까운 r 차원 근사 행렬입니다. 즉, 원래 데이터의 구조를 최대한 유지하면서 차원을 줄인 표현이에요. 여기서 r은 남길 특잇값의 개수를 뜻합니다.

 

예를 들어, 1000×1000 픽셀 크기의 이미지를 하나의 행렬이 있다고 가정해 볼게요. 이 행렬에서 상위 50개의 특잇값만 남겨도 원본 이미지와 거의 구별하기 어려운 수준으로 이미지를 복원할 수 있습니다. 이는 대부분의 정보가 소수의 주요 축(특이벡터 방향)에 집중되어 있다는 점을 이용한 거예요. 이처럼 SVD 기반 차원 축소는 정보 손실을 최소화하면서도 표현을 단순하게 만드는 데 효과적입니다.

이번 주 뉴스레터에서는 머신러닝과 관련된 확률과 선형대수학의 핵심 개념들을 살펴봤어요. 본문에서 자세히 다루진 않았지만, 최적화 이론 역시 빼놓을 수 없는 중요한 요소입니다. 머신러닝에서는 보통 손실 함수를 최소화하는 게 핵심인데, 그 중 대표적인 방법이 바로 경사 하강법(Gradient Descent)이에요.

 

결국 머신러닝은 수학적인 모델링 위에 세워진 분야이기 때문에, 수학은 그 기초를 이해하는 데 큰 도움이 됩니다. 혹시 주변에 "인공지능은 관심 있는데, 왜 수학을 알아야 해?" 하고 고민하는 분이 계시다면, 이번 뉴스레터를 살짝 공유해보는 건 어떨까요? 😉

-

SNS를 팔로우하면

최신 소식을 가장 빠르게 확인하실 수 있습니다 😆

지금 읽고 있는 뉴스레터를 매주 받아 보고 싶다면

아래 '구독하기' 버튼을 클릭해주세요 😉

📬 <위클리 딥 다이브> 구독하기